
Un problème d'optimisation combinatoire est un problème où il faut minimiser une certaine fonction (dite de coût) sur un ensemble fini de configurations.
Nombre de ces problèmes peuvent se poser en termes de graphe. Un graphe est composé d'un ensemble fini de points et d'un certain nombre de liens (orientés ou non) reliant ces points. De plus, à chacun de ces liens peut-être associé un poids. Par exemple, on peut considérer le graphe suivant : les points sont les aéroports du monde entier, les liens sont les liaisons qui existent et les poids sont le temps de vol (ou encore la distance ou le prix du voyage).
Après quelques exemples, j'explique comment on peut définir la complexité d'un problème d'optimisation combinatoire. Vous pouvez, si vous le voulez, sauter les exemples.
On considère le graphe suivant : un ensemble de N points (ici N = 10) dans le carré unité, les liens (non orientés) sont tous les couples de points possibles, pondérés par la distance entre ces points (il y a donc N(N-1)/2 liens).

1. Le problème du voyageur de commerce
Le problème du voyageur de commerce (Travelling Salesman Problem (TSP)) est le suivant : un voyageur de commerce doit passer une fois et une seule dans un certain nombre de villes, il désire faire le moins de chemin possible.
L'ensemble des configurations est l'ensemble des chemins fermés passant par tous les points et la fonction de coût est la longueur de ces chemins. Une configuration est donc caractérisée par la donnée de N liens.
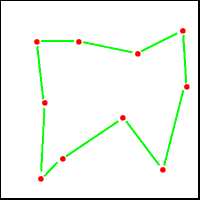
C'est un problème très difficile à résoudre (voir plus loin). On propose une liste de site intéressant sur la résolution de TSP.
2. Le problème d'appariement minimal
Le problème d'appariement minimal (Minimun Matching Problem (MMP)) est le suivant : il s'agit d'apparier les points deux à deux (il en faut donc un nombre pair) de façon que la longueur totale de l'appariement soit minimale.
L'ensemble des configurations est constitué d'appariements c'est-à-dire de configurations où chaque point est relié à un et un seul autre point (une configuration acceptable est donc composée de N/2 liens). La fonction de coût est la somme des longueurs des liens de l'appariement.
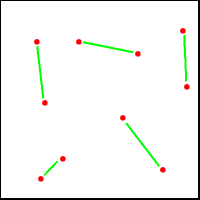
Ce problème est beaucoup plus simple que le précédent (voir plus loin). c'est pour cette raison que je m'y intéresse tout particulièrement (dans sa version stochastique).
3. L'arbre couvrant minimal
Le problème de l'arbre couvrant minimal (Minimum Spanning Tree (MST)) consiste à trouver l'arbre passant par tous les points (d'où le nom) dont la somme des longueurs des liens est minimale.
L'ensemble des configurations est l'ensemble des arbres couvrants, c'est-à-dire l'ensemble des configurations constituées de N-1 liens et telles qu'il existe toujours un chemin entre deux points quelconques.
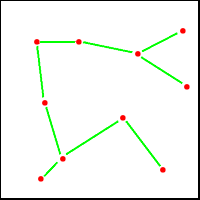
Ce probème est le plus simple des trois.
Pour résoudre un problème d'optimisation combinatoire on utilise un algorithme. Un exemple d'algorithme qui marche pour n'importe quel problème d'optimisation combinatoire est le suivant : on essaye toutes les configurations possibles et on choisit celle qui minimise la fonction de coût. Néanmoins bien que cet algorithme soit très simple en théorie, il ne peut pas être utilisé dans la majorité des cas car le nombre de configurations, bien que fini, est très souvent gigantesque. Par exemple, pour le voyageur de commerce, il y a (N-1)!/2 configurations, ce qui fait 181440 pour N = 10 et 4.67 10155 pour N = 100.
Cet exemple nous incite à définir la complexité d'un algorithme comme étant le nombre d'opérations à effectuer pour résoudre le problème. En fait on ne va s'intéresser qu'à la façon dont ce nombre augmente avec la taille des données (pour un graphe ce sera le nombre N de points). Ainsi pour le voyageur de commerce, les meilleurs algorithmes que l'on connaisse voient leur complexité augmenter comme une exponentielle de N. En revanche pour l'appariement minimal le meilleur algorithme a une complexité en N3. Et pour l'arbre couvrant minimal le meilleur algorithme est en N2log(N).
La distinction fondamentale que l'on fait pour distinguer les différents problèmes d'optimisation combinatoire est le suivant : connaît-on un algorithme pour résoudre le problème dont la complexité soit au plus polynomiale en N ? Si c'est le cas le problème sera un problème P (P comme polynomial), sinon ce sera un problème NP. (Note pour les puristes : ce n'est pas vraiment la définition de P et de NP mais en gros ça revient à ça). Ainsi le voyageur de commerce est NP alors que l'appariement minimal et l'arbre couvrant minimal sont P.
Pour bien comprendre la différence de difficulté entre les différentes complexités voici un petit tableau dans lequel j'ai mis le temps qu'il faut pour résoudre un problème de complexité donnée (en supposant que l'on fait 1000 opérations par seconde).
| Complexité | N = 1 | N = 10 | N = 100 | N = 1000 | N = 10000 |
|---|---|---|---|---|---|
| log N | 0 ms | 1 ms | 2 ms | 3 ms | 4 ms |
| N | 1 ms | 10 ms | 0.1 s | 1 s | 10 s |
| N2 | 1 ms | 0.1 s | 10 s | 17 min | 28 heures |
| N3 | 1 ms | 1 s | 17 min | 12 jours | 32 ans |
| eN | 3 ms | 22 s | 9 1032 ans ! | longtemps | très longtemps |