DEUG MIAS

Complexité

Travaux pratiques

Chronomètrage de function, procedure et autres. (Valable sur Codewarrior 1.3)

Problèmes de mémoires

Tableaux, Appel récursif sur tableaux, Structures, pointeurs, ensembles

Exercice 1.

Le tri à bulle.

Il s'agit de présenter expérimentalement la notion de complexitè.

On fournit les grandes lignes de la mèthode. Les élèves élaborent l'algorithme. Ils doivent visualiser les parties réalisées en temps constant (noté co) ainsi que la variable dont dépend le temps de calcul (içi n le nombre de valeurs à trier). En fonction de cela on trouvera que T(n) le temps de calcul de cet algorithme est tel que,

T(n)=c0*n(n-1)/2

L'algorithme:

pour j de n-1 à 1 faire

pour i de 1 à j faire

si v[i]>v[i+1] alors

permut(i,i+1)/* réalisée en temps constant noté c0*/

fin

fin

Correction

Exercice 2.

Le tri par insertion.

Amener les étudiants à concevoir un algorithme de tri par insertion. Sur celui-ci isoler les parties réalisées en temps constant. Attention insister sur la nature de la complexité: le pire cas; ie on suppose que l'on passera dans chaqu'une des parties constantes...

Début

Pour i de n à 2 faire

max=vect[1] /* i */

indice=1 /* ii*/

Pour j de 2 à i faire

Si vect[j]>max alors /* iii */

max=vect[j] /*iv */

indice=j /* v */

finSi

fin Pour

echange(vect,i,indice)/* vi */

fin Pour

fin

Les lignes i à vi sont des lignes réalisées en temps constants. On note c0 les temps i +ii +vi et c1 les temps iii+iv+v. On a alors le temps t de cet algorithme qui s'exprime de la manière suivante :

Rappel: n+(n-1)+(n-2)+...+1=n(n+1)/2

d'ou

t=(c0+c1*(n-2) )+(c0+c1*(n-3))+(c0+c1*(n-4))+ ... +(c0+c1) +c0= c0*(n-2)+c1*(n-1)(n-2)/2=(n²)

Exercice 3.

Elaborer un tri de complexité linéaire en plaçant certaines contraintes. Amener les élèves à trouver ces contraintes. Mettre en évidence que la lecture du vecteur trié n'est pas forcement linéaire.

Exercice 4.

Un bon exemple de récursion est le tri rapide (quicksort), inventé par C.A.R. Hoare en 1962. Etant donné un tableau, on choisit un élément noté x dans celui-ci et on répartit les autres en deux sous-ensembles - ceux qui sont inférieurs à x et ceux qui lui sont supérieurs ou égaux. On applique ce même processus à ces deux sous-ensembles, récursssivement. Lorsqu'un sous-ensemble a moins de 2 éléments, ce n'est pas la peine de le trier, ce qui arrête la récurssion.

On peut içi choisir de partager tous les sous-ensembles par rapport à leur élément central.

Corrigé

(Pascal)

(C)

Exercice 5.

Dans cette exercice on ne programmera pas d'algorithme. On s'appuiera seulement sur des exemples concrets pour mettre en évidence la différence entre les algorithme précédents (dans P) et certains dans NP-complet. Précisement il s'agit de présenter un algorithme de complexité exponentiel: énumération des k-colorations, puis exhiber les colorations valides complexité en (m*kn) , n=|V| et m=|E|.

Exercice 6.

On présentera deux algorithmes. L'algorithme 'glouton' de coloration de graphes et si possible DSATUR de Brélaz..

 

Début GLOUTON

G=(V,E)

Y=V

couleur=0

Tant que YØ Faire

couleur=couleur + 1

Z=Y

Tant que ZØ Faire

i=min{j | 1jn et v_j Z}

colorier v_i par couleur

Y=Y-v_i

Z=Z-v_i-{les voisins de v_i}

Fin

Fin

Fin GLOUTON

 

1. Que réalise cet algorithme. Que représente l'ensemble Y ainsi que Z. Qu'elle est la propriété des sommets sélectionnées dans la boucle interne. Fixer la notion de cliques, le partionnement des sommets d'un graphe en différentes cliques, le lien avec la coloration des sommets d'un graphe.

2. Evaluation de la complexité de Glouton en dans le pire des cas. Recherche des taches réalisées en temps constant.

3. Les graphes planaires. la conjecture de la 4-coloration des MPG5.

4. Colorier le graphe MPG5 suivant par Glouton. Conclusion: Glouton trouve une 5-coloration, mais ce graphe est 4-coloriable. Exhiber une 4-coloration. Lien avec Glouton dans P et la solution pas forcement exacte, seulement approchée.

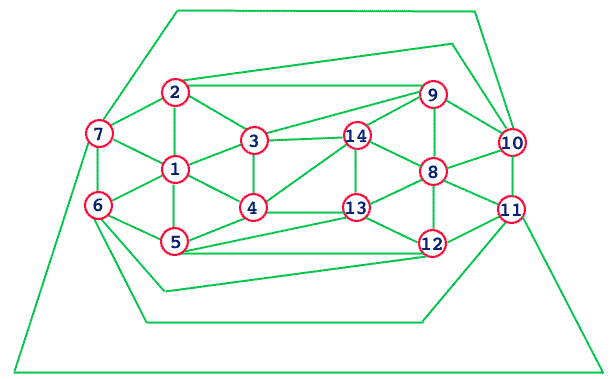
5. Si possible présenter DSATUR.

prolland@ices.fr - 05/98