Que calculer sur un ordinateur ?

On cherche à savoir ce qu'il est possible de calculer sur un ordinateur.

Les questions que l'on peut se poser :

Qu'est-ce que calculable signifie ?

Qu'est-ce que l'on entend par ordinateur?

D'autre part, on veut en restant général, rendre compte de la réalité (et du futur si possible) des ordinateurs; pour cela on définira la machine abstraite de Turing.

Un résultat important est qu'il existe des fonctions que l'on ne peut calculer, ie il existe des problèmes qui ne sont pas calculable sur ordinateur maintenant et dans le futur !!!

Au dela des limites théorique, il existe des limites pratiques de temps et d'espace. La question de ce qui est calculable en pratique semble être directement liée à la technologie du jour. Pourtant, il est possible de distinguer dans l'absolu des problème qui ont une solution " faisable " (en anglais: tractable) et des problèmes qui ont certes une solution, mais demandant des calculs si coûteux en temps qu'ils sont irréalisables. Par exemple, le jeu d'échecs est un jeu à deux joueurs à information complète. On sait qu'il existe un algorithme de jeu optimal. En pratique, l'explosion combinatoire fait que l'on ne peut pas calculer l'ensemble, pourtant fini, de toutes les parties possibles.
Nous introduirons une mesure de la complexité d'un algorithme en comptant le nombre d'opérations élémentaires qu'il faut effectuer en fonction de la taille des données. Si cette fonction est au moins exponentielle, le problème cesse très rapidement d'être traitable. Par contre, si cette fonction est au pire polynomiale, on dira que le problème reste faisable.

On vient de voir deux problèmes connexes face à la résolution d'un problème

la qualité de sa résolution (aspect théorique): la calculabilité, la décidabilité

la quantité en espace et temps(aspect pratique ): la complexité

Pour l'aspect théorique, les deux notions calculabilité et décidabilité sont d'une certaine manière des notions connexes.

Notions abordées de manière introductive

Alphabet

Langage

Type de machines

Machine de reconnaissance de langage

Machine de réalisation de fonction

Machine d'énumération de langage

Modèle de calcul

Définition d'un problème

Définition de la résolution de problème

Equivalence résolution de problème et reconnaissance de langage

Exemple de problème faisable, non faisable

 

Alphabet

En informatique, on manipule toujours des objets finis qui appartiennent à des ensembles tout au plus infinis dénombrables. De plus, les objets manipulés le sont toujours via une représentation. Ainsi, les nombres entiers par exemple ne sont jamais manipulés directement: dans le langage courant, 1989 est un entier, mais en fait il s'agit ici d'une chaîne de quatre caractères, sur l'alphabet décimal {0,1,2,3,4,5,6,7,8,9}, qui est l'une des multiples représentations possibles de ce nombre. Ce qui est manipulé est la représentation dans la base dix de ce nombre et non le nombre lui-même. Nous allons faire l'hypothèse, pour notre étude, que les seuls objets manipulés sont des mots sur des alphabets finis, mots qu'on est libre ensuite d'interpréter comme la représentation d'objets d'une autre nature.

Définition:
Un alphabet X est un ensemble fini de symboles ou lettres. Un mot sur l'alphabet X est une suite finie de lettres de l'alphabet. La longueur du mot est le nombre de lettres que comporte ce mot. Le produit de concaténation de deux mots est une opération qui consiste à mettre les deux mots bout à bout. Ce produit confère à l'ensemble de tous les mots sur X, noté X*, une structure de monoïde, dont l'élément neutre est le mot de longueur nulle, appelé mot vide.

Un alphabet étant donné, on définit une relation d'ordre totale sur X* de la façon suivante: on se donne un ordre arbitraire sur les lettres de l'alphabet, et on ordonne alors les mots selon un ordre, appelé ordre hiérarchique, en les ordonnant d'abord selon les longueurs puis selon l'ordre alphabétique (dit aussi: lexicographique) induit par l'ordre sur les lettres.

Ainsi si X={a,b,c} avec a<b<c, et en notantle mot vide, on peut numèroter (en rouge) les mots (en bleu) de X* de la façon indiquée ci-dessous:

Langage

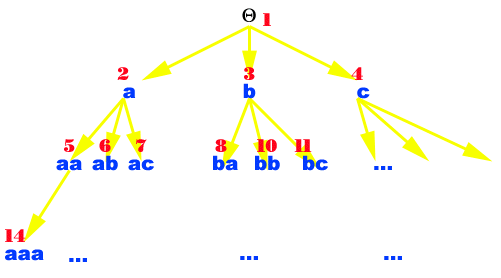
Soit A* un monoïde libre engendré par l'alphabet A. Un langage est une partie de A*.

Les types de machines
En entrée de la machine, on fournit une ou plusieurs données, en sortie on obtient un résultat. Ici, nous prendrons comme hypothèse que les données sont entrées sous la forme d'une suite de caractéres (c'est ainsi qu'on entre au clavier des données), i.e. un mot sur un certain alphabet. Le résultat est un élément d'un ensemble prédéfini. Nous distinguerons, selon la nature de cet ensemble plusieurs types de machines:

Machine de reconnaissance de langage

S'il s'agit d'un ensemble à deux éléments, par exemple {oui, non}, ou bien {0,1}, la machine permet de séparer les données en trois parties en fonction du résultat: l'ensemble des mots sur l'alphabet d'entrée pour lesquels la machine donne l'un des résultats, l'ensemble des mots sur l'alphabet d'entrée pour lesquels la machine donne l'autre résultat, ainsi que l'ensemble des mots sur l'alphabet d'entrée pour lesquels la machine ne donne pas de résultat. Ces ensembles constituent des langages; les deux premiers sont complémentaires si la machine fournit un résultat pour toute donnée. On parlera alors de machine de reconnaissance. Le critère de la décidabilité repose sur ce type de machine.

Machine de réalisation de fonctions

S'il s'agit d'une suite finie de caractère celle-ci forme un mot sur un certain alphabet Y. Si X est l'alphabet d'entrée, la machine définit une fonction f de X* dans Y*: la fonction qui à un mot w en entrée associe le mot en sortie de la machine si celle-ci fournit un résultat pour cette donnée. On dira que la machine réalise la fonction f. Si la machine fournit un résultat pour toute donnée, cette fonction est totale.
Notons que le premier type que nous avons distingué n'est en fait qu'un cas particulier du second.

Machine d'énumération de langages

S'il s'agit d'une suite non bornée de caractères, cela n'a évidemment d'intérêt que si celle-ci s'écrit sur un alphabet ayant au moins deux lettres, et en considérant l'une de ces lettres comme un séparateur, on obtient comme résultat une suite de mots (séparés par le séparateur) qui constituent un langage. On dit alors que ce langage est énuméré par la machine.

Plutôt que de changer complètement de machine à chaque fois que l'on change de problème, on va définir des classes de machines ayant toutes les mêmes principes de fonctionnement et ne différant que par le programme.

Modèle de machine

On appellera modèle de calcul la description de toutes les opérations élémentaires qu'on peut effectuer: sur quels objets et comment agissent chacune d'elles, ainsi que la description de comment on indique à la machine, par le programme, l'ordre dans lequel elle doit exécuter les opérations. Une instance du modèle est une machine particulière qui fonctionne comme il est indiqué par le modèle. Cette machine est définie par la donnée de son programme:

modèle + programme = machine

Un modèle de calcul étant défini, la question se pose de savoir quelle est la classe des langages qui peuvent être reconnus par une machine instance de ce modèle, qu'on appellera une -machine (respectivement: la classe des fonctions qui peuvent être réalisées, la classe des langages qui peuvent être énumérés). Ces langages (respectivement: ces fonctions, ces langages) seront dits -reconnaissables (respectivement -calculables, -énumérables).

Dans la suite on s'interressera aux problème des langages qui peuvent être reconnus par une machine de reconnaissance. Ce choix n'est pas contraignant car ce que peut réaliser les deux autres types machines, la machine de reconnaissance peut le faire. La seule différence est dans la description des entrées et des sorties pour chacune d'entres elles. Par exemple, on peut très bien imaginer une machine R de reconnaissance qui reconnaisse tous les mots du langage énuméré par une machine d'énumération E; ie M réponde OUI si le mot appartient au langage énuméré par E, et NON sinon.

Définition d'un problème

Un problème est constitué par:

(1) la description de la représentation (finie) des éléments d'un ensemble
fini ou infini dénombrable,
(2) un énoncé portant sur les éléments de cet ensemble, énoncé qui peut être
soit vrai, soit faux selon l'élément choisi.

Exemples:

PROBLÈME 1:
Donnée: un entier écrit en base dix.
Question: cet entier est-il premier ?

PROBLÈME 2:
Donnée: un entier écrit en base dix.
Question: cet entier s'écrit-il comme la somme de 4 carrés ?

PROBLÈME 3:
Donnée: un entier écrit sous la forme du produit de ses diviseurs, eux-mêmes écrits en base dix.
Question: cet entier est-il premier ?

PROBLÈME 4:
Donnée: un graphe fini représenté par la liste de ses sommets, suivie de laliste de ses arcs, chaque sommet étant représenté par un entier écrit en base dix.
Question: ce graphe admet-il un chemin hamiltonien ?

PROBLÈME 5:
Donnée: une suite finie de couples de mots (u₁,v₁), (u₂,v₂), etc. (u_k,v_k).
Question: Existe-t-il une suite d'indices i₁, i₂, ...,i_n telle que

u_i1,u_i2,...u_in=v_i1,v_i2,..v_in

Equivalence résolution de problème et reconnaissance de langage

La représentation explicite des données est une composante du problème (cela est notamment très important lorsqu'on s'intéresse à la complexité d'un problème). Chaque donnée constitue une instance du problème. Elle est représentée par un mot sur un alphabet fini.
A chaque problème, constitué donc d'une représentation des éléments d'un ensemble et d'un énoncé portant sur ceux-ci, est naturellement associé un langage, appelé langage caractéristique du problème, constitué de l'ensemble des mots qui sont la représentation d'un élément de l'ensemble pour lequel la question admet pour réponse: vrai.
On notera Lp le langage caractéristique du problème P.

Etant donné un problème P, le problème contraire CP est le problème obtenu à partir de P en gardant la même représentation des données et en prenant l'énoncé contraire. Par exemple, le problème contraire du problème 1 est le problème:

PROBLÈME: Donnée: un entier écrit en base dix;
Question: cet entier est-il non premier ?

La résolution d'un problème se ramène donc à la reconnaissance d'un langage: le langage associé à ce problème. On pose donc la définition formelle suivante:

Définition: Une machine résout un problème P si et seulement si pour tout mot f représentation d'un élément de l'ensemble considéré par ce problème, elle permet de déterminer, en un temps fini, si ce mot appartient à Lp ou à Lcp.

On classe les problèmes en fonction de la difficulté (en un sens qui sera précisé par la suite) qu'il y a à donner la réponse en fonction de la donnée. Un problème est trivial si Lp = Ø ou si Lcp = Ø. En effet, dans ce cas, il n'est même pas utile de connaître la donnée pour donner la réponse. Attention, ce qui est trivial c'est de donner la réponse, mais il peut être très difficile de démontrer que le problème est trivial en ce sens.

Exemple de problème faisable et non faisable

Par exemple, le problème 2 est trivial. Les problèmes 1 et 3 comportent la même question; pourtant le problème 3 se résout beaucoup plus facilement: à la simple lecture de la donnée, on peut donner le résultat, alors que dans le problème 1 il est nécessaire de faire subir un traitement à la donnée. Le problème 4 est plus complexe: on ne connaît aucune méthode qui fonctionne de façon déterministe en temps polynomial pour résoudre ce problème; en d'autre terme ce problème est NP-complet. Enfin, le problème 5 est un problème que l'on ne peut pas résoudre au sens indiqué. Ce problème s'appelle le problème de correspondance de Post, il est indécidable, ie son langage associé n'est pas récursif, il est soit récursif énumérable ou pas.