Complexité en temps dans le pire cas de

triRapide

Mis à part les appels récurssifs, ainsi que la boucle interne for(i=gauche+1;i<=droit;i++) noté B, les instructions de la fonctions triRapide sont réalisées en temps constant; la procedure echanger est clairement executée en temps constant. On note q le facteur constant représentant la somme des temps constants de la boucle interne B et p les autres temps constants. Pour évaluer le temps consommé par cette fonction par rapport à la taille n de l'instance initiale, il faut alors :

1. Enumérer le nombre k d'appels récurssifs

2. Pour chacun de ces appels hors appels récurssifs il y a p+(q*(droite-gauche)) temps consommé.

Il reste donc à énumérer le nombre d'appel récurssif.

procedure triRapide ( var vect : myArray ; gauche, droit : integer ) ;

var

i, dernier : integer;

begin

if(gauche<droit) then

begin

echanger(vect,gauche,(gauche+droit) div 2);

dernier := gauche;

for i:=gauche+1 to droit do

if (vect[i]<vect[gauche]) then

echanger(vect,++dernier,i);

echanger(vect,gauche,dernier);

triRapide(vect,gauche,dernier-1);

triRapide(vect,dernier+1,droit);

end ;

end;

 

Tout le source.

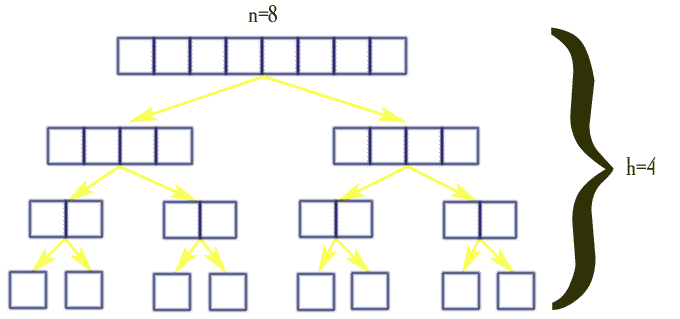
Initialement gauche=1 et droite=n. On peut alors énumérer ainsi:

Niveau	Nombre d'instructions élémentaires par niveau
Premier niveau (n=8)	p+(q*(n))
Second niveau	2*{p+(q*n/2)}
Troisième niveau	4*{p+(q*n/4)}
...	...
h-1	2h-2*{p+(q*n/(2h-2))}
Dernier niveau h	n

Majoration de h

On peut modéliser l'ensemble des appels de la fonction triRapide par une arbre binaire équilibré. Si h désigne la hauteur minimum de l'arbre binaire alors

 2^h-2n2^h-1

D'où

hlg₂(n)+2

Remarques

Les opérations effectuées sur le niveau h sont en faite réalisées toutes en temps constant car il s'agit uniquement du test suivant:

if(gauche>=droit)

return;

Ainsi à ce niveau il y a n conditions executées. C'est tout.

Conclusion

On calcule la somme des opérations élémentaires sur les h niveaux. On note P= p+2p+4p+...2^h-2*p et Q=(h-1)*(q*n). On a alors une complexité en temps T en P+Q, ie

TP+k₁(n*lg₂(n))

où k₁ est une constante. La somme P est la somme des élément d'une suite geometrique de raison 2 et de premier terme U⁰=1. Alors

1+2+4+8+16+...+2^h=U⁰+U¹+U²+U³+..+U^h

=2⁰+2¹+2²+2³+2⁴+...+2^h

=(2^(h+1)-1)/(2-1)

=2^(h+1) -1

de plus, on peut remarquer que

1+2=4-1

1+2+4=8-1

1+2+4+8=16-1

soit 1+2+4+8+16+...+2^h = 2^(h+1) -1 !!!!!

Ainsi P= p * (2^(h-1) -1). Puisque 2^lg₂(x)=x on a :

Tk₂n+k₁(n*lg₂(n))

où k₂ est une constante. D'où

T=(n*lg₂(n))